Now this is a bit wordy and a bit technical but please bear with it, it's interesting - honestly!
Most procurements of significant value will be by tenders evaluated using a Most Advantageous Tender (MAT) evaluation model. This evaluates tenders for quality elements as well as price. The evaluation methodology must be stated in the invitation to tender and purchasers aren't allowed to move away from the published model nor may they 'develop' the methodology after the evaluation methodology is published. This is a problem when evaluation panels decide that they are going to award, say, up to two points for training initiatives, up to three points for added value and up to five points for value for money when these sub elements have not been published in the methodology. This will be the subject of a future post but for now let's concentrate on the price evaluation.
It is quite typical for evaluation models to split the overall score between price and quality in a 40:60 ratio, or 50:50, or even 60:40. The choice of ratio will be dependent on the subject of the procurement and in some cases it may go as high as 80:20.
In the quality elements the scoring may run from 1 to 10 in grades that are described in the methodology and so it is quite possible for tenderers to achieve a high quality element score.
In contrast pricing evaluation is quite commonly evaluated by comparing the individual prices against the price bid by the lowest priced tender (when there is a purchase involved, when the tender is for a disposal the comparison is with the highest price, of course).
This comparison is often done using the formula:
Score = (max score) x (Lowest price/Actual price) (*in graph below)
Putting some figures into this will demonstrate its use more clearly. Let's say the price element is 40% of the overall score (the other 60% being awarded for various quality elements); Tender A bids £425, Tender B bids £500. Tender A scores 40% x 425/425, ie 40%. Tender B scores 40% x 425/500, ie 34%.
That looks okay, the score of the higher priced tender is reduced from the full score available and a tender that's even higher priced will score even less (try it, a £600 tender will score only 28.33%). And for many practitioners this seems to be quite acceptable. However, see what happens when the price bid is twice that of the lowest priced. Let's try Tender C who bids £850. In this case the score is 20%. If Tender D goes up to £1000, the score only falls to 17%. It gets worse. If Tender E bids £100,000 they still score 0.17%.
Does this matter? If the price is that far away from the lowest bid they're unlikely to be in contention anyway. Well I think it does matter. We have explored the extremes to find the weakness of the formula, however the weakness is still there when the prices bid are closer to each other - it's just that it doesn't hit us in the face.
This evaluation model makes the difference in price increasingly less relevant.
An alternative is to use the pricing formula:
Score = (max score) - (((Actual price - Lowest price)/Lowest price) x Max score) (**in graph below)
Putting in the scores for the Tenders A - F we get:
A £425 40% (was 40%)
B £500 32.94% (was 34%)
C £850 0% (was 20%)
D £1000 -14.12% (was 17%)
E £100,000 -9332% (was 0.17%)
Putting this on a graph the difference can be seen graphically, and the linear nature of the alternative formula can also be clearly seen.
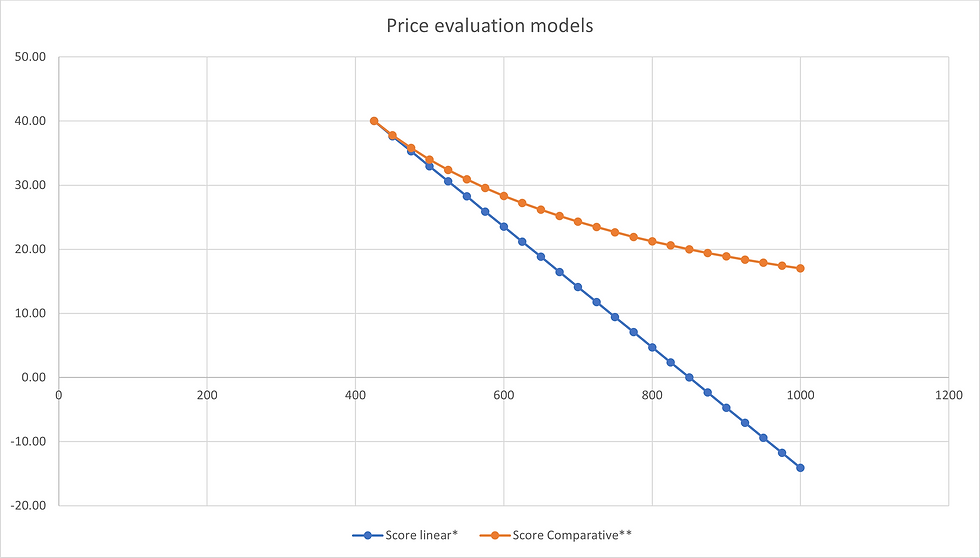
This linear approach does mean that some tenders score negative values in the price score but this reflects the cost benefit of lower tenders much more accurately. Some practitioners place a minimum score of zero to avoid negative scores. This approach is not new but it is also not widely used. The comparative approach is more easily explained but is inequitable.
If you would like to talk about tendering and tender evaluation please get in touch.
Comments